統計的有意とはなにものか
― ベイズ統計学による分析 ―
永井宏幸 Nagai Koko(市民科学研究室・低線量被曝研究会)
PDFはこちらから
アブストラクト
疫学の分析でよく使われる仮説検定では,有意水準を与えれば統計的有意かどうかが自動的・機械的に判定される.しかし,判定の結果を日常的な言語で伝えようとすると極めて曖昧であることが露呈してしまう.判定結果の解釈において誤解と混乱が生じていることは否定しようがない現実である.それはフィッシャー統計学の限界を示すものである.
本稿では仮説検定を使い放射線リスクを分析した重要な論文をとりあげて,そのデータをベイズ統計学を使って分析することによって,両者を比較し,仮説検定のもつ問題を明らかにするとともに,ベイズ統計学による放射線リスクの評価方法が開発されることを願ってひとつの試みを提供する.
1. 仮説検定と統計的有意
仮説検定はフィッシャー統計学が提供するツールのうちの最も実用性があり,放射線リスクの疫学的分析でも標準的アプローチであるかのように多用されている.その方法を素描すると,検定したい仮説(帰無仮説という)の正しい母集団を仮定して,これから無作為に抽出した標本の集団を考え,標本と母集団の中心の‘距離’を定義する.‘距離’の定義は簡単でないがp値という指標で代用する.p値は‘距離’が離れるにつれて小さくなる.データはこの標本のひとつである.検定に先立って有意水準というp値の基準値を決めておき,データのp値がこれより小さいとき,データが母集団の中心から‘離れすぎている’と考え,帰無仮説が否定されたと判定する.このとき「帰無仮説が棄却された」と表現する.仮説検定では帰無仮説に対置する対立仮説を設定しておくので,これは「対立仮説が統計的に有意に認められた」と表現する.リスク分析では帰無仮説に「リスクなし」をとり対立仮説に「リスクあり」をとる.有意でない場合はデータと母集団の中心の‘隔たり’は統計的な揺らぎによるとみなすということになる.有意でないときそれをどのようにリスク評価の言葉で表現するかは曖昧である.単に帰無仮説の否定ができなかったとする解釈と,積極的に帰無仮説を採用すべきことを示しているとする解釈がある.この曖昧さは統計学の教科書でもみられ,専門家の間でも統一した解釈がない.ここには仮説検定のもつ重大な欠陥が集約的に現れている.それが社会に及ぼしている弊害はとてつもなく大きいものと考えられる.この論考の主題はここにある.
まず放射線影響研究所のLSS14次報告書(2012年)を取り上げて,仮説検定が放射線疫学でどのように使われているかを具体的にみることにする[ ].この報告書は広島・長崎原爆被爆者のLSSコホートの1950年から2003年までの死亡率を分析したもので,主たる分析の方法は直線モデルにより相対過剰リスク係数ERR/Gyを求め,βが95%信頼区間の全域でβ>0であればリスクが統計的に有意であるという判定を下すというものを採用している.この論考では報告書が扱った死因のうち固形がんに集中して論じる.
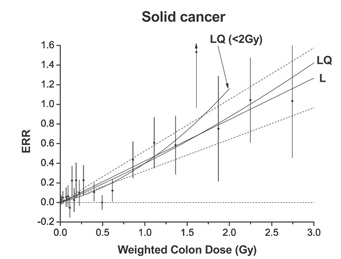
図1 固形がんのERRと95%CI.Lは1次モデルの回帰直線.LQは1次+2次モデルの回帰曲線.x軸はDS02にもとづく結腸の被曝線量.論文Fig.5.
以降, LSS14次報告書を単に論文と書くことにする.
論文には分析結果が階級化した被曝線量におけるERRの点推定と95%信頼区間を示すグラフで報告されている(図1に転載).グラフには1次モデルの回帰直線とその95%信頼区間が示されている(実線Lと点線).また(1+2次)モデルの回帰曲線と,2Gy未満に線量を限ったときの回帰曲線も示されている.LとLQの間に有意差がないことから1次モデルによるβの推定値0.42と95%信頼区間0.32-0.53の値を採用して,固形がん死亡率が被曝線量とともに統計的有意に増加していると結論している.
次に論文は,低線量域でもこの有意性が成り立つかどうかを調べている.結果は図2に引用してある.x軸は線量域の上限の値であり,たとえば0.2Gyのプロットは0Gyから0.2Gyの線量域で求めたβを示している.有意かどうかは95%信頼区間の下限値から判定している.グラフが示すように,0.2Gy以上では有意であり0.1Gy以下では有意でない.論文は,この分析結果と,別に行った閾値の分析の結果を総合して,「有意なERRをもつ最小の線量は線量域0から0.2Gyであり,閾値の分析により閾値はないと推定する」という結論をえている.
【続きは上記PDFでお読み下さい】
