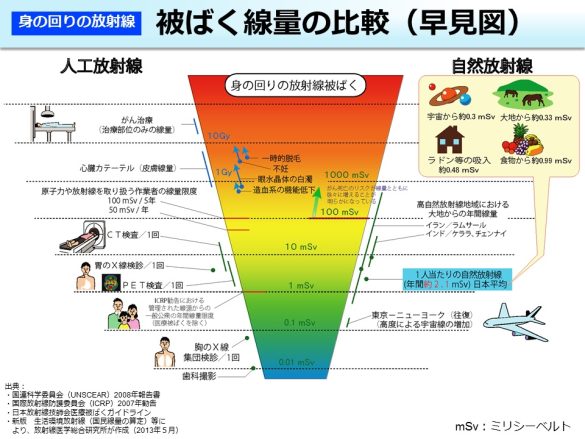
100ミリシーベルト以下の放射線のリスクはよく分かっていない、という説明を聞いたことがありませんか。さらには100ミリシーベルト以下の放射線など心配しなくていいという説明なんかも。
こうした誤った説明の出所をたどると放射線医学研究所（放医研）に辿り着きます。
放医研はホームページで「放射線被ばく早見図」を掲載していますが、100ミリシーベルト以下のリスクについて触れていません。
私たち低線量被曝研究会はこのことに疑問をもち放医研に質問書を送って見解をただしました（こちらのページにその質問と回答を掲載しています）。
やり取りで明らかになったことを紙芝居の形にして公開することにしました。
以前に公開した第2版（2024年7月1日、初版は2022年12月13日）を改訂した「第2.1版」を以下に掲載しています（以下の図をクリックすると開きます）。
また、英語版も公開しています（以下の英語版の図をクリックすると開きます）。なお、紙芝居の英訳には市民研会員の武智ゆりさんに，スライドへの流し込みには市民研会員の谷俊一郎さんに協力をいただきました．
質問と回答についてはこちらにもまとめました。
なお、紙芝居はpdfファイルのものを公開していいますが、スライドショーのファイル（pptxファイル）も用意しているので入手を希望される方はご連絡ください。
教室での先生と生徒の会話ですので読みやすいと思います。
ご感想などを知らせていただくと幸いです。
> リスク の確率を直接計算する統計によれば「統計的に有意」になるのはリス
> クのある確率が97.5%以上のばあいなんだ
このロジックは、『雨の降る確率が20%であるとき，傘を持っていかないと雨にぬれる確率は20%ですが傘を持っていかないと邪魔になる確率が80%あるということです．』に由来しているそうです。
疑問点
・非ベイズ統計のp値（帰無仮説の元でそのデータセットが得られる確率）とベイズ統計で求めた確率（対立仮説が正しい確率）の点推定値は同じ（同じ（ように扱える）であれば、その説明で良いと思います）？
有意水準と比較するp値は帰無仮説のもとで観察データが得られる確率であり、
「統計的に有意」になる「リスクのある確率」とは関係ないのではないでしょうか。
差のある事象が検定で失敗せずに検出できるかどうかは、
タイプ2エラーの大きさで決定（どれだけのパワーで検定できるかどうか）されるのではないでしょうか。
リスクと向き合う困難さは、甲状腺検査のリスクがないと信じたい気持ちとも共通しているのではないでしょうか（より問題を俯瞰的に扱ってはどうか）。
・仮説検定は何らかの確率を計算して判定する手法
・ベイズ統計では仮説が成り立つ確率を直接計算できる。そこで帰無仮説が成り立つ（表現が良くないかもしれません）確率と対立仮説が成り立つ確率（対立仮説が帰無仮説の余事象であれば引き算で求まる）を計算して判定することが考えられる。
・この考え方では、第1種の誤りの確率（もっとも安全評価では第二種の誤りの制御がより重要になる）が制御できていない。このため、事後オッズ比を用いる方法が考案されているがこの方法は、事前分布に依存する。そこで、ベイズファクターを用いる方法が考案されている。
いずれにしても誤りの制御の観点でのトレードオフに帰着する課題となるのではないでしょうか。
トレードオフ分析では視点や前提も重要になる。
甲斐 倫明, 山田 崇裕, 橋本 周, 山本 正史, 山田 憲和, 酒井 宏隆, 荻野 晴之, 米原 英典, 服部 隆利, 山口 一郎, 佐々木 道也, 日本保健物理学会2021年度企画シンポジウム国際対応委員会セッション「IAEA DS499（免除）及びDS500（クリアランス）の動向と論点―総合討論」, 保健物理, 2021, 56 巻, 3 号, p. 156-159, 公開日 2022/01/06, Online ISSN 1884-7560, Print ISSN 0367-6110, https://doi.org/10.5453/jhps.56.156
ここでの資料の作成には富山大学の「富山から考える震災・復興学」を受講なさっているみなさまにも協力を得ています。
1月14日付で山口一郎氏が投稿した疑問点について「紙芝居」制作者のひとりとして見解を投稿します．
（疑問) 非ベイズ統計のp値（帰無仮説の元でそのデータセットが得られる確率）とベイズ統計で求めた確率（対立仮説が正しい確率）の点推定値は同じ（同じ（ように扱える）であれば、その説明で良いと思います）？
（見解) p値は帰無仮説の下でそのデータが得られる確率ではありません．またベイズ統計が求めるのは確率（対立仮説が正しい確率）ではなく変数βの確率密度(確率分布)です．
（疑問) 有意水準と比較するp値は帰無仮説のもとで観察データが得られる確率であり、「統計的に有意」になる「リスクのある確率」とは関係ないのではないでしょうか。」
（見解) 非ベイズ統計のp値はデータが得られる確率ではありません．このようなp値についての誤解が広がっていることを統計学者は危惧しています．誤ったp値の理解を広めるようなことは慎んでほしいものです．（あるデータがえられる確率はゼロなのです．）
（疑問) 差のある事象が検定で失敗せずに検出できるかどうかは、タイプ2エラーの大きさで決定（どれだけのパワーで検定できるかどうか）されるのではないでしょうか。
（見解) 非ベイズ統計では，差が本当はないのに仮説検定で差があると判定してしまうのをタイプ1エラー，差が本当はあるのに差がないと判定してしまうのをタイプ2エラーとよびます．前者の大きさはp値で，後者の大きさは検出力という量で与えられると考えます．このような概念が必要になるのは，仮説検定の出力が仮説が有意に棄却されるか否かの≪決定≫であるからです．ベイズ統計学では出力が確率密度です．たとえばリスクがあると考えるかないものと考えるかは，確率密度をもとに決めることになります．このときの判断は統計学とは独立に社会的・倫理的観点から総合的におこなうことになります．非ベイズ統計のように機械的に判断することにはなりません．
いつも丁寧にご説明くださり有り難うございます。
『（見解) p値は帰無仮説の下でそのデータが得られる確率ではありません』
ご指摘ありがとうございます。確率値であるp値とは、帰無仮説の下でそのデータよりも偏りのある（帰無仮説から遠ざかる方向の）データが得られる確率ですね。表現を端折りすぎてしまいました。この誤りは、どのような誤解を招く恐れがありそうでしょうか？
『またベイズ統計が求めるのは確率（対立仮説が正しい確率）ではなく変数βの確率密度(確率分布)です．』
仰るようにベイズ統計が求めるは、確率密度(確率分布)です。確率分布上のそれぞれの点を計算するイメージを持ってしまっていました（この考え方の不適切な点をご指摘をいただけませんか？）。『（あるデータがえられる確率はゼロなのです．）』とあるのも仰るとおりだと思います。申し訳ございません。
ここでの「点推定値」は、確率密度(確率分布)上の点帰無仮説をイメージしていましたが、永井さんに教えて頂きたいのは、ベイズ統計による判定と仮説検定の違いです。
『このような概念が必要になるのは，仮説検定の出力が仮説が有意に棄却されるか否かの≪決定≫であるからです．』
「帰無仮説」が「有意に棄却されるか」の判定のあり方に限らず、何らかの判定を試みる際に直面する課題は、どのようなエラーを制御するかに帰着するのではないでしょうか。
『このときの判断は統計学とは独立に社会的・倫理的観点から総合的におこなうことになります．非ベイズ統計のように機械的に判断することにはなりません．』
非ベイズ統計だと1-βが0.8以上である前提でpが0.05を下回るかどうかを機械的に判定する（効果量なども吟味せずに）ということでしょうか？
政策的な判断を下す際には、用いる統計学の手法に限らず、「社会的・倫理的観点から総合的におこなう」ことになるのではないでしょうか。