連載
21世紀にふさわしい経済学を求めて
第12回
桑垣 豊(NPO法人市民科学研究室・特任研究員)
PDFはこちらから
「21世紀にふさわしい経済学を求めて」のこれまでの連載分は以下からお読みいただけます。
第1章 経済学はどのような学問であるべきか (第1回から)
第2章 需給ギャップの経済学 保存則と因果律 (第2回から)
第3章 需要不足の原因とその対策 (第4回から)
第4章 供給不足の原因と対策 (第6回から)
第5章 金融と外国為替市場 (第8回から)
第6章 物価変動と需給ギャップ(第10回から)
第7章 市場メカニズム 基礎編(第11回から)
7-5 市場タイプ別モデル
ここまでは、財・サービス市場を想定して、市場モデルを築くことをこころみた。ここからは、市場タイプ別に、価格分布のある需要供給分析がどのように適用できるかを説明する。基本的には、需要(買い手)側から見た「販売率(売買成立率)」と、実際の「売上価格分布」をあらわす式をあげる。売上価格分布というのは、どの価格がどれくらいの割合で実際に売れたかをあらわしている。
1)財・サービス市場(卸売市場を含む)
a)売り切れのない場合
これはすでに述べた通りであるが、基本になるので(1)(3)式を再掲載する。
販売率は
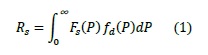
売上価格分布は
![]()
(3)式と少し違うのは、s(供給)とd(需要)が入れかわっていることである。しかし、売上価格分布は、売り切れがない限り数学的には変わらない。同じ販売率を使ったほうが分かりやすいので、この形にした。
抽象的すぎてわかりにくいので、具体的計算例で説明する。需要(買い手)側は、平均して単価3万円、標準偏差が5000円の購入上限価格の分布をしているものとして、売り手がどのような価格を設定すればいいか、という問題を考える。図7-3の例では、販売価格として平均3万4000円、標準偏差6800円で売るとする。メーカーが定価(小売希望価格)を4万円5000円ぐらいとしても、小売店ではこのようなバラツキができてしまうような場合である。ここでは、仮に正規分布であるとした。アンケートなどで、具体的な分布がわかっていれば、それを使えばいい。全供給数(生産台数)や全需要数(買いたい人の延べ人数)などの詳しい設定は、表7-1にまとめた。
上記の数式に従って、計算(数値積分)した結果を図7-3に示した。「数量密度分布」とは、縦軸が密度関数に全供給数や全需要数を掛け算したものになっている。これで、供給と需要の大きさが同じグラフで比べることができる。
表7-1 供給平均価格3万4000円の場合(図7-3に対応)

図7-3 財・サービス市場の価格分布(需要・供給・売上)
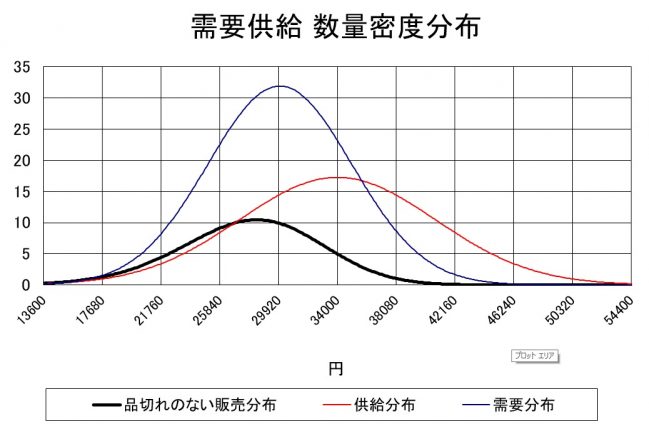
需要の平均価格より、供給の平均価格が4000円高いので、供給量の40%しか売れない。需要量から見ると販売率は30%。グラフの販売分布の価格の低い部分が供給部分よりも上回っているのは、もっと高い価格でも買う人が安い店に出会う確率が一定あるからである。
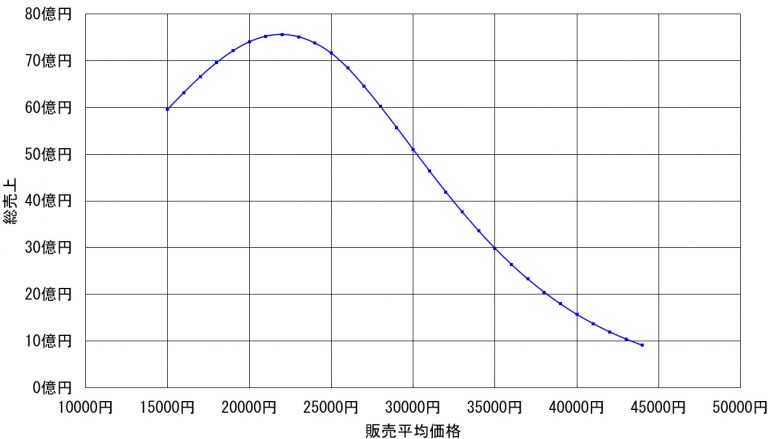
これは供給側の設定した価格分布の一例にすぎないので、もっと安くすればどうなるであろうか。図7-4は、供給平均価格を1万5000円から1000円きざみで、図7-3のような計算を30パターン繰り返して、その総売上がどう変化するかを見たものである。全供給数は、全生産総額が100億円になるようにしている。需要側の設定はすべて同じであるが、供給側はそのほかに標準偏差を平均価格の20%になるようにした。
その結果、もっとも売上額が大きいのは供給平均価格が2万2000円のときであることがわかる。もちろん、生産台数が変わるので生産コストも変化する。利益が最大になるのは2万2000円ではないかも知れないが、コストのほうも別に計算して総売上から引き算すれば、もっとも利益が大きくなる価格設定ができることになる。
問題を複雑にしないために、メーカーは一社独占で流通過程で価格が分散する場合をあつかった。複数のメーカーが価格によるマーケティング戦略を練るときの場合は、第8章の応用編で取り上げる。
図7-4 販売設定価格と総売上の関係
b)売り切れのある場合
実は上記の式では、買い手が多すぎる売り切れの場合は求まらない。売れ残りの場合は、店頭や在庫にたくさんの商品があっても次の日に売ればいいので、生鮮食品のように持ち越しのできない商品を除いて問題にはならない。長期的には、なかなか売れなければ、入荷量を減らし在庫を処分することになる。現代の大量生産の社会では、通常はたくさんの商品を用意しているので、売り切れは少なく、買い手の動向が売れ行きを決めることが多い。
それでも、ときどきある売り切れの場合はどうなるか考えてみる。ここで言う売り切れとは、自分で買える価格よりも低い価格設定をしている店ではあるが、売り切れている場合である。自分で買える価格よりも高い価格設定をしている店で、売り切れていても元々買わないので、売り切れとは見なさない。
【思考実験】
一日間の売れ行きを考えてみる。日の初めに在庫を補充したら、後は商品が売れて在庫が減り続けるとする。だれかが、一つ商品を買ったとすると、供給価格分布も需要価格分布も、その売れた価格のところだけ1つ分分布が小さくなる。すると分布が変わったので、その新しい価格分布で商品のその後の売れ行きを計算し直す。
初めの一つ目の商品の取り引き価格は、この価格分布のある市場モデルでは、事前には確率的にしかわからない。1つ目の商品で計算した「売上分布×販売率」で、需給分布それぞれを、「供給分布」は[1÷全在庫量]、「需要分布」は[1÷全需要量]だけ縮める。分割できない一つの商品を、確率に従って割り振るなんて「量子力学」みたいだと思われる方もいるかも知れない。「売上分布」と、「供給分布」「需要分布」は異なるので、計算後の「供給分布」「需要分布」は形が少し変わる。次の計算のための密度関数は、全価格帯で積分したときに1になるように調整する。この調整は、数学的処理なので気にしないでいただきたい。
大変ややこしくて恐縮であるが、この計算を一日の需要数だけ繰り返す。そうすると需要がすべて売上になるように見えるが、そのつど販売率(0と1の間)を掛けるので、売上にならない需要も計算に入れている(買い損ない)。供給分布は安い価格帯のところが減ってきて、全体の販売率が下がって行く。これを、売り切れがだんだん多くなって行くことだと見なす。
パソコンでプログラムすれば、このような計算は可能であるが、もっと簡易な方法はないのであろうか。まず、「a)売り切れのない場合」の方法で1回計算する。その結果、売上数予測が在庫(供給)総数よりも多ければ、在庫総数で打ち切る。売上価格分布はそのまま採用する。分母だけ在庫総数にして、どの価格帯でどれくらい売れるかの分布はそのまま。
しかし、価格条件のミスマッチを考えると、用意した商品が全部(全供給量)売れるはずがない。そこで需要側の販売率(購入率というべきか)を全供給量に掛け算するという便宜的な方法を採用する。購入率は、全需要中の実際の売上数の割合であるから変だが、現実的ではないであろうか。
商品ごとに経験を積み重ねて検証するしかない。数字があわないとしても、簡単な補正方法がみつかればいい。また、供給量が需要の何%を下回れば、上記の便宜的方法に切り替えるか基準が必要である。将来、機会を得られれば、検証してみたいものである。
【続きは上記PDFでお読み下さい】
市民科学研究室の活動は皆様からのご支援で成り立っています。『市民研通信』の記事論文の執筆や発行も同様です。もしこの記事や論文を興味深いと感じていただけるのであれば、ぜひ以下のサイトからワンコイン(100円)でのカンパをお願いします。小さな力が集まって世の中を変えていく確かな力となる―そんな営みの一歩だと思っていただければありがたいです。
