連載

21世紀にふさわしい経済学を求めて

第 31 回

桑垣豊　（NPO 法人市民学研究室・特任研究員）

PDFはこちらから

【これまでの連載（掲載ページへのリンク）】

第1回　第2回     第3回      第4回      第5回      第6回      第7回      第8回　第9回

第10回  第11回　第12回　第13回　第14回　 第15回　 第16回　 第17回　第18回

第19回　 第20回　　第21回　　第22回 　第23回　 第24回　第25回　第26回  第27回

第28回    第29回　第30回

第１章    経済学はどのような学問であるべきか　（第1回）

第２章    需給ギャップの経済学 保存則と因果律　（第2回と第3回）

第３章    需要不足の原因とその対策　（第4回と第5回）

第４章    供給不足の原因と対策　（第6回）　番外編　経済問答その1（第6回と第7回）

第５章    金融と外国為替市場　（第8回と第9回）

第６章    物価変動と需給ギャップ（第10回）

第７章    市場メカニズム　基礎編（第11回と第12回）

第８章    市場メカニズム　応用編（第13回）　番外編　経済問答その2（第13回と第14回）

第９章    労働と賃金（第15回）

第10章   経済政策と制御理論（第16回）

第11章  経済活動の起原（第17回と第19回）　番外編  経済問答その3（第18回）

第12章  需要不足の日本経済史（第20回と第21回）　番外編　経済問題その4（第22回）

第13章　産業関連分析（第23回）

第14章　武器取引とマクロ経済(第24回)　番外編　経済問答その5（第25回）

第15章　植物進化に学ぶ（第26回）

番外編　解説＆経済問答その６「株式市場」（第27回）

番外編　解説＆経済問答その７「資産選択理論への疑問」（第28回）

番外編　解説＆経済問答その８「資産運用立国？」　（第29回）

第16章　年金は何のためにあるのか（第30回）

第17章　統計学と経済学

統計学は数値をあつかうときはもちろん、アンケートのような選択肢の回答を集計するときにも必要です。当然、経済学にも必要ですが、使い方があやしい。でも今回説明するのは、今の経済学での使い方を検証して、正しい方法を示すのは一部だけです。

経済学であつかう予測の値打ちはどれくらいか、みかけの周期と意味のある周期の見分け方、気象学で使っている確率的予報（アンサンブル予報）の応用などを紹介します。

今回の話は、むずかしいと言えばむずかしい話です。書くのは結論だけにしてしまえば、簡単かも知れません。そうすると、「なるほど、そういうことか。しかし、常識的なことばかりで、どこが目新しいのかな」と思われてしまいそうです。常識的なことは、その理由もそれほどむずかしくないのではないか。統計学を使うときはやり方さえわかっていたらいい、と思うかも知れません。

しかし、それがそんなに簡単ではないのが統計学です。統計学を使うときにもっとも頭を悩ませるのは、分析対象に対して、どんな方法を使ったらいいかがわからないことです。それ以前に、使うべきときに、こんな単純なことに統計学を使わなくてもいいと思ってしまいがちです。

最近、世論調査で選択肢の回答率の％を小数点以下１桁であらわすようになりました。例えば12.3％のように。これは、有効数字が３桁であることを意識したものです。その選択肢を選んだ人が1000人未満だと、割り算の２つの数の有効数字が小さいほうの数字で有効数字を考えないといけないからです。小学校６年で習うはずですが、みんな忘れてしまいます。今まで細かい数字の違いを気にして、誤差の範囲の大小を、意味のある違いとして大きく取り上げていました。

今回はむずかしい話や、いろいろ数式が出てきたりしますが、それはそんなもんだと思って、読み飛ばしてもらってもかまいません。ただし、人によってどこまでわかるか、様々なので、一通り載せることにしました。わかるところまで、読んでください。

これでも、数学者や統計学者、物理学者には、初歩的に見える内容です。そのせいか、今回書くことは、あまり本に載っていなかったり、簡単にしか書いてなかったりします。かと言って、中学校で習う数学でもわかるようにするには、高校の数学教科書、丸写しにたくさんのページをさく必要があるので、そこまではできませんでした。

また、今回とりあげたような数少ないことを書いている本が、間違っていることもあります。そういうことで、あえて今回はむずかしいことも載せることにしました。経済の連載ですから、経済学者が間違った方法を避ける手助けになる、とひそかに考えています。

今回の構成

17－１　クロス集計

17－２　予測と情報量

17－３　格差論争と分散分析

17－４　周期性（規則性）の検証

17－５　アンサンブル予測

クロス集計は今回の導入編で、きちんと分析するには案外簡単そうに見えるときにも、ふさわしい統計学の方法が必要だという話です。

予測の話は、的中率は同じでも、珍しい現象のほうが予測には価値があることを説明します。裏返して言うと、的中率が高くても意味のない予測もあるということです。その予測の値打ちが数字（情報量）であらわせるというのがミソです。

格差論争は、21世紀に入った頃にあった日本の格差論争が、統計学を無視して進み、まちがった結論で決着したのではないかと問います。

周期性と言えば、経済では景気の好況・不況の周期に注目が集まっています。経済学では周期性と言わず、循環と言っています。循環では必ず元に近い状態に戻る印象があるので、もっと一般化して周期性と呼ぶことにします。今回は、分かりやすい例として、富士山の噴火と地震の周期性を取り上げます。地震学会の発生確率予測にも疑問を投げかけます。

アンサンブル予報と言えば難しそうですが、台風の進路を予報円であらわすときに使っています。本当は、円でなく楕円で表示するべきだという話をします。経済予測で説明するにはデータ集めが大変で、計算も複雑になりすぎるので、説明には台風の進路予想を使います。それも、かなり単純化したモデル計算をします。それでも、「確率分布の合成」という微分積分の計算が必要です。数学的な部分は付録にしますので、読み飛ばしてください。これは、この連載史上もっともむずかしく、数式の連続です。

でも、数学の応用に関心のある方には、宇宙物理など各種シミュレーション計算で大変役立つ方法です。ネットや本で調べても、まとめて書いた本はありません。数学の部分だけなら、よい本が１冊だけ見つかりました。付録のところで紹介します。

ところで、すでにこの連載で紹介した統計的手法もあります。第７章の「価格分布のある市場モデル」と、第10章の「制御理論」です。統計学に関心のある方は、そのような目で読み返していただけると幸いです。

17－１　クロス集計

統計学はむずかしいので、どうしても必要なときだけ使えばいい、と考える人が多いかも知れません。しかし、かなり単純に見える場合にも使わなければいけないのに、使っていないだけのことがたくさんあります。

例えば、アンケートの分析で、10才きざみの年齢層別で回答数を比べるとき、その年齢層の中での回答を％であらわします。これをクロス集計分析と言います。分析するとき、この％どうしで比べるのですが、少し（例えば0.1％）でも違えば、違うと言えるかどうかはサンプル数によって変わってきます。新聞の世論調査などでは、単純に％の数字の大小だけでコメントをつけるのが普通です。それでは、誤差の範囲の違いを、意味のある違い（有意）にしてしまうかも知れません。

この場合は、カイ二乗検定という分析方法を使うことになっていますが、これでは年齢全体と回答の関係はわかっても、個々の20代、30代、……ごとの特徴はわかりません。それには一工夫して、２×２の単純な分割表に置き換えて分析することになるのですが、ほとんどだれもやっていません。やるにしても、この２×２分割表をカイ二乗検定で分析してしまいますが、結構誤差があるので危険です。

では、ふさわしい方法はというと、カイ二乗検定のイエーツの補正（誤差が少ない）や、フィッシャーの直接法（誤差がない）が正確です。フィッシャーの直接法は、電卓・そろばん時代には計算が大変でした。そのかわりに仕方なく誤差は大きくてもカイ二乗検定を使っていたのです。イエーツの補正なら大して計算は増えないので、使うべきなのに知らない人が大半です。

それにフィッシャーの直接法は、40年前くらいのパソコンでもすぐ計算できます。サンプル数が増えて、例えば１万にもなると大変な計算になるなどと、ネットを調べると書いてありますが、対数を使えば一瞬です。実は、フィッシャーの直接法は超幾何分布という名前だけ難しそうな分布を使う分析法ですが、Excelには超幾何分布の関数があるので、少し工夫すれば一瞬で計算してくれます。

　●クロス集計の例

理屈だけではわけがわからない、という人も多いでしょう。具体的なアンケートの例で考えます。ある高校で、就職するなら学校関係と金融機関では、どちらに就職したいかを聞いたとします。表の上と下では、回答の割合は性別でまったく同じですが、調査した人数（サンプル数）が上のほうがちょうど２倍になっています。

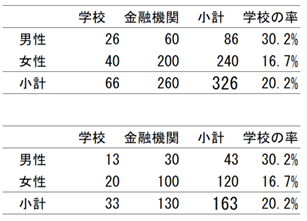
表17－１　クロス集計の例

そこで、統計分析（検定）が必要になります。表17－２は、「カイ二乗（χ²）検定」と「フィッシャーの直接法」で同じ集計結果に対して、検定を行なった結果です。仮説は「性別で回答に違いはない」というもので、％はその仮説が正しい率をあらわしています。％が少ないということは、「違いがない確率が低い」＝「違いがある確率が高い」ということです。こういう証明したいことと反対の仮説を立てて、それを否定することで証明する方法が「帰無仮説」による分析です。正面から証明するほうがむずかしいので、このような手のこんだ方法を使います。

表では、分析方法とサンプル数によって％が違います。サンプル数が326人のときは、いずれも％が低いので、性別によって回答に違いがあるという結論です。しかし、サンプル数を半分にして分析してみると、５％をはさんだ割合になっています。この％のことを有意水準といいます。通常５％未満で「違いがある」とします。検定方法によって差が出てしまいました。もっと結論を出すのを厳しくするときは、１％水準や0.1％水準のこともあります。

フィッシャー法のほうが正確な検定方法であることがわかっているので、サンプル数が少ないと、カイ二乗検定の誤差が大きくなることがわかります。カイ二乗検定では、サンプル数が50未満とか100未満で誤差が大きくなると言いますが、この例ではそれより多くても無視できない誤差があります。

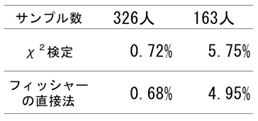
表17－２　分析方法を比べる　％は有意水準

統計学の入門書には、この場合の計算方法がまだカイ二乗検定で書いてあることが多く、フィッシャーの直接法が載っていることもありますが、おまけで書いてあります。新しい入門書でも、統計学の初歩は内容が確定していることになっているので、昔の本と内容を変えていません。計算方法が進歩すれば、それを入門書にも反影させないといけません。それをサボっているのです。そして、それに従って統計ソフトも昔の方法のままで、使う人も分析方法を意識しないので、それがずっと続くのです。

ちなみに、直接法のフィッシャーは統計学者で、経済学者のフィッシャーとは別人です。お間違えなく。

【参考文献】

『分割表の統計解析』宮川雅巳、青木敏　朝倉書店　2018年　2900円

　クロス集計表（分割表）の分析方法は「カイ二乗分析で決まり」と思っている人が多い中、統計学的にどう考えるべきかを書いた珍しい本です。この本によると、統計学者の間では常識的な内容だが、それを解説した分割表の本がないので、この本を出版することにしたとあります。今回の連載でむずかしいこともあえて取り上げたことと、共通しています。

17－２　予測と情報量

リーマンショックは、１００年に一度の危機であったといいます。来年は危機ではないと毎年予想して、１００年に１回、予想がはずれて危機がおとずれても、的中率は99％だと言ったりします。しかし、このような予測に意味があるのでしょうか。その予測が持っている情報量を計算することで、その価値を求めます。

まず、発生確率だけがわかっている場合の情報量を算出します。次に、予測の的中率を加味して、発生確率だけがわかっているとき以上の情報が得られる予測であるか、どうかを調べます。

情報量は、確率の逆数を２の何乗になるか（２を底とする対数）で表わします。例えば、12.5％の確率（的中率）だと、８分の１なので逆数は８。８は２の３乗（２×２×２）なので、情報量は３になります。でも、的中率まで考えて、予測の情報量をどうやって求めるのでしょうか。具体的な数字を使って、計算してみます。先に情報量の公式を示しますが、数式が苦手な人は読み飛ばしてください。

１行目の式が、情報量ｈの計算方法です。雨の降る確率が12.5％だとすると、先ほどの計算のように情報量は３になります。エントロピーＨは、その情報量に同じ確率を掛けて、全部の場合を足しあわせて求めます。全体の情報量と思ってください。的中率を考えるときは、はずれる確率の分の情報量を引き算して計算します。

　　式(1)

• 天気予報の例

数式だけで考えてもむずかしいので、次の計算例を見てください。１週間のうち、５日が晴で、２日が雨の単純なモデルを考えます。予報ではなく、晴れと雨の割合がわかっているとして、その情報量です。情報量は0.863になりますが、右の表のように半々の確率のときがもっとも情報量が多くて、片寄るほど情報量が減ります。

この割合は現実にそうなっているということなので、半々から離れるほど情報の値打ちがない、ということではありません。また、エントロピーを乱雑さととらえて、マイナスの値だとして引き算し、(－1.000)－(－0.836)＝＋0.137を情報量とすることがありますが、まちがいです。物理学（熱力学）の話と混同しています。

表17－３　天気割合の情報量

今度は、的中率も考慮に入れて計算してみましょう。

的中率については、的中率の負の情報量を求めて、元の情報量から引き算します。例えば、的中率1/2なら、情報量１をマイナスと見なします。式(1)の１行目、確率のところに的中率を代入します。的中率が低いほど、情報量ｈは大きくなります。不確実性の部分を情報量から取り除いたことになります。

表17－４の左側は、晴と雨の割合は表17－３と同じですが、晴の予報は５回に１回、雨は２回に１回予報がはずれる場合の計算です。例えば、日本の天気の基本パターンは、５日晴れて２日雨が続きます。現実には、これからはずれることも多く、曇りや雪もあります。話を簡単にしました。

予報の方法は、例えば「明日の天気は今日と同じ」という単純なものを考えます。天気のパターンが、５日晴れて２日雨を正確に繰り返しているとします。そうすると、晴れの予報は５回に１回、雨は２回に１回はずれることになります。

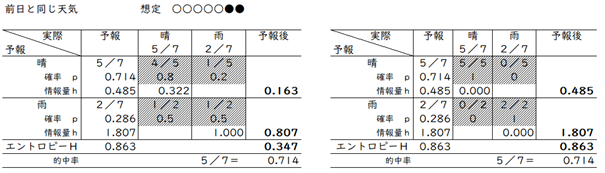
表17－４　天気予報の情報量

右側は、的中率１００％の場合です。表17－３左と同じになることがわかります。この場合も、天気割合と天気予報の情報量を比べて、天気割合のほうが値打ちがあると解釈してはまちがいです。同じ予報の中で、的中率が高いほど予報の価値つまり情報量が多いと見るべきです。

ところで、左の情報量0.347は、何を意味しているのでしょうか。天気に連続性があるという情報を使っていて、その値打ちが情報量0.347だということです。これよりも的中率が下がれば、情報量がマイナスになることもあります。そうすると、予報をしないほうがいいことになります。

• 経済予測の例

リーマンショックのような経済「危機がある」という予報は、天気予報の雨よりも確率が低く100分の１なので情報量が6.644と大きくなります。一方、「危機がない」という予想の情報量は、もともと実現確率が高いので、情報量はわずか0.0145にすぎません。これは、それぞれの予報を出して的中したときの情報量です。的中率を考慮して予報を評価すると、どうなるでしょうか。もし、危機と予想したときの的中率が、危機のおきる確率と同じ１％だすると、全体としての情報量はほぼゼロになります。表17－５を見てください。

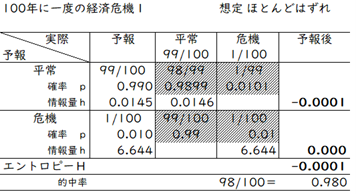
表17－５　経済危機の情報量１

しかし、危機のおきる予想を１００年に２回して、50％の確率で当たるとします。表17－６を見ると、全体としての情報量は0.107ですが、危機を予想した場合に限ると極めて高い情報量であることがわかります。２回に１回でも危機を予想できれば、大きな価値があるからです。的中率98％は同じなのに。

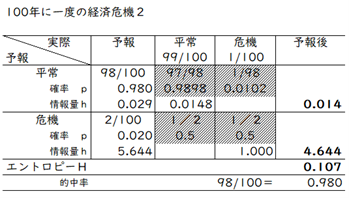
表17－６　経済危機の情報量２

この計算では、危機を予想できたときの利益（損失の縮小）や、予想がはずれたときの損失などの利得表がないので、実際の予想の価値を見積もることはできません。損得まで考えると、危機を予想する２回のうち１回あたるというのは大変なことです。単純な的中率の計算に惑わされないために、必要な知識です。

【参考文献】

『情報数学のはなし 改訂版』大村平　日科技連出版社　2018年　P38など参照

　著者は、航空自衛隊のトップ、元航空幕僚長。ずっと技術畑を歩いて来られたようです。大村さんのおかげで、航空自衛隊の事故が少なくてすんでいるのかも知れません。情報数学だけで一冊の本は、この本だけのようです。大変参考になりますが、「予想割合の評価」と「的中率を考慮した計算法」がまちがっていました。今回書いた部分は全面的に関係するので、一から考え直しました。

17－３　格差論争と分散分析

かつて、経済学界で格差論争がありました。日本の所得格差は、同志社大学橘木（たいばなき）教授が以前と比べて実質的に増えたと主張し、大阪大学大竹教授は増えたように見えても見かけにすぎないと言い、論争になりました。経済学界では、見かけにすぎないという主張が正しいとして決着しました。これを統計学の知識で考察すると、逆転するのではないかという話をします。

ジニ係数などの分散をあらわす指標には、気をつけないといけません。それは、層別に分散（標準偏差、ジニ係数）を求めて、それを重みづけ平均しても全体の分散を求めることはできない点です。層の間の分散も取り入れないと、全体の分散が計算できないからです。分散分析のひとつ一元配置分析の方法を知れば、理解できます。

【続きは上記PDFファイルでお読みください】